Timeline

2025-03-07

I got as far as the “howManyBits” problem.

2025-03-07

I finished it. Once again, I feel this experiment is quite good.

Recently, as a teaching assistant for the computer system course, I need to check students’ completion of this CSAPP experiment. I did this experiment during my undergraduate studies, but I’ve basically forgotten everything after so long. So, I’m doing it again and recording the process here.

Experiment Environment Setup

I completed this in the Windows 10 WSL2 environment:

实验环境

For detailed instructions on setting up the environment, please refer to the following link. There is a script for one-click environment setup, which is very convenient:

CSAPP Environment Setup

https://zhuanlan.zhihu.com/p/505497911

Introduction

Complete the function implementations in bits.c, but there are certain restrictions on the code.

1
2
3
4
5
6
# Check whether the code complies with the required specifications
./dlc bits.c
# View score
make clean 
make 
./btest

Experiment Content

bitXor

Problem:

1
2
3
4
5
6
7
8
9
10
/* 
 * bitXor - x^y using only ~ and & 
 *   Example: bitXor(4, 5) = 1
 *   Legal ops: ~ &
 *   Max ops: 14
 *   Rating: 1
 */
int bitXor(int x, int y) { 
  return 2;
}

The requirement is to implement XOR using only ~(Bitwise NOT) and &(Bitwise AND). You may use equivalence calculus from discrete mathematics. XOR means ‘0 if the bits are the same, 1 if different’:

1
2
3
int bitXor(int x, int y) { 
  return ( ~(~x & ~y)) & (~(x & y));
}

tmin

Problem:

1
2
3
4
5
6
7
8
9
/* 
 * tmin - return minimum two's complement integer 
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 4
 *   Rating: 1
 */
int tmin(void) {
  return 2;
}

Returns the smallest two’s complement integer. The definitions of sign-magnitude, one’s complement, and two’s complement are as follows:

Representation Definition
Sign-magnitude The most significant bit is the sign bit (0 indicates positive, 1 indicates negative), and the remaining bits represent the absolute value.
One’s complement For positive numbers, the one’s complement is the same as the sign-magnitude; for negative numbers, the sign bit remains unchanged, and the other bits are bitwise inverted.
Two’s complement For positive numbers, the two’s complement is the same as the sign-magnitude; for negative numbers, the two’s complement is the one’s complement plus 1.

Two’s complement encoding is asymmetric. Except for the smallest negative number, every negative number corresponds to a positive number. On a 64-bit system, the range of integers represented in two’s complement is:

  • Smallest negative number: 0x8000000000000000 (i.e., -2^63).
  • Maximum positive number: 0x7FFFFFFFFFFFFFFF (i.e., 2^63 - 1)
1
2
3
int tmin(void) {
  return 1 << 31;
}

isTmax

Problem:

1
2
3
4
5
6
7
8
9
10
/*
 * isTmax - returns 1 if x is the maximum, two's complement number,
 *     and 0 otherwise 
 *   Legal ops: ! ~ & ^ | +
 *   Max ops: 10
 *   Rating: 1
 */
int isTmax(int x) {
  return 2;
}

  • Returns 1 if x is the maximum two’s complement value; otherwise, returns 0.
  • The maximum value is 0x7FFFFFFF, characterized by the most significant bit being 0 and all others being 1, so 0x7FFFFFFFbecomes 0x8 after adding +0x1. 00000000, with the most significant bit being 1 and all others 0, which is exactly the opposite.
  • Here, we need to use the property of XOR, such as x^target. After inverting x and XORing it with target, since XOR outputs 1 for differing bits and 0 for identical bits, only when x and target are exactly the same will x^target be 0x0. Then, by applying the ! operator, we get !(x^target), which is 1 when x equals target and 0 otherwise.
    For 0x7FFFFFFF, after adding 1, it becomes 0x80000000, due to the opposite characteristic, after bitwise NOT, it becomes 0x7FFFFFFF, so we can use XOR to check if they are the same, that is: !(~(x+1) ^ x).
  • Keep thinking: is it only 0x7FFFFFFFthat satisfies this property, where adding 1 is equivalent to bitwise NOT? Obviously, 0xFFFFFFFFalso satisfies this property, because when overflow occurs, the most significant bit is discarded, resulting in 0x0. Therefore, we need to construct an expression combined with !(~(x+1) ^ x), called expression1, i.e., !(~(x+1) ^ x) & expression1. When x is 0x7,FFFFFFFexpression1 equals 1, and when x is 0xFFFFFFFFit equals 0.
  • The exclusion method must use 0x7. FFFFFFFThere is 0xFFFFFFFFThe characteristic of lacking 0, that is, the difference between these two numbers, and the simplest difference is 0x7. FFFFFFFbecomes 0x8 after adding +0x1. FFFFFFFIt is a non-zero number, and 0xFFFFFFFFbecomes 0 after adding 0x1. Therefore, !(x+1) is 0 when x is 0x7. FFFFFFFand is 1 when x is 0xFFFFFFFF!(x+1) is exactly the opposite of what is needed, so adding a NOT operation suffices, that is: 
1
2
3
int isTmax(int x) {
  return !( ~(x + 1) ^ x) & !!(x + 1);
}

allOddBits

Problem:

1
2
3
4
5
6
7
8
9
10
11
/* 
 * allOddBits - return 1 if all odd-numbered bits in word set to 1
 *   where bits are numbered from 0 (least significant) to 31 (most significant)
 *   Examples allOddBits(0xFFFFFFFD) = 0, allOddBits(0xAAAAAAAA) = 1
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 12
 *   Rating: 2
 */
int allOddBits(int x) {
  return 2;
}

  • Returns 1 if all odd-numbered bit positions are 1; otherwise, returns 0. That is, if the 1st, 3rd, 5th, 7th, and so on bits of a number are 1 (regardless of other bits), it returns 1; otherwise, it returns 0.
  • We can eliminate the influence of all even-numbered bits and focus on the odd bits, for example, by performing x & 0xAAAAAAAAUsing bitwise AND, all even bits become 0; then check whether it equals 0xAAAAAAAAthe same (as explained in isTmax, using bitwise AND to determine if two numbers are identical). Alternatively, you can let x and 0x55555555bitwise OR, so all even bits become 1; then check whether it equals 0xFFFFFFFFthe same. That is:
  • However, due to the experiment’s constraints, you cannot directly write 0xAAAAAAAAlike this; you can only write 0xAA and obtain 0x through bitwise operationsAAAAAAAA

Note: According to the C standard, shift operations have lower precedence than addition and subtraction.

https://en.cppreference.com/w/c/language/operator_precedence

1
2
3
4
5
6
7
8
int allOddBits(int x) {
  // return !((x|0x55555555)^0xFFFFFFFF);
  // return !((x&0xAAAAAAAA)^(0xAAAAAAAA));
  int a = 0xAA<<8;//0x00AA
  int b = a | 0xAA;//0xAAAA
  int c = b<<16 | b;//0xAAAAAAAA
  return !((x&c)^c);
}

negate

Problem:

1
2
3
4
5
6
7
8
9
10
/* 
 * negate - return -x 
 *   Example: negate(1) = -1.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 5
 *   Rating: 2
 */
int negate(int x) { 
  return 2;
}

  • Return the negative of x.
  • We know:
  • Subtracting the two expressions yields: 
    1
    2
    3
    int negate(int x) { 
      return ~x+1;
    }

    isAsciiDigit

    Problem:
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    /* 
     * isAsciiDigit - return 1 if 0x30 <= x <= 0x39 (ASCII codes for characters '0' to '9')
     *   Example: isAsciiDigit(0x35) = 1.
     *            isAsciiDigit(0x3a) = 0.
     *            isAsciiDigit(0x05) = 0.
     *   Legal ops: ! ~ & ^ | + << >>
     *   Max ops: 15
     *   Rating: 3
     */
    int isAsciiDigit(int x) {
      return 2;
    }
  • To check whether x is an ASCII digit, simply determine if x is between 0x30 and 0x39.
  • In assembly, comparisons are performed by subtraction which sets the flags. Therefore, we can subtract x from 0x30 and 0x39 respectively and check the sign bit to verify: 0x30 - x should be less than or equal to 0 with the sign bit set to 1, and 0x39 - x should be greater than or equal to 0 with the sign bit 0. However, if x is at the boundary, for example x == 0x30, then 0x30 - x equals 0 with the sign bit 0, which also satisfies the condition. Hence, we can replace <= with <: This is equivalent to: Now, does the right side x < 0x39 require an equivalent transformation? Since 0x39 - x should be greater than or equal to 0 with the sign bit 0, and if 0x39 - x < 0 the sign bit is 1, analyzing the boundary conditions shows it is inclusive, so no equivalent transformation is needed (transforming it would exclude the boundary condition).
    To ensure the sign bit of 0x2F - x is 1 and the sign bit of 0x39 - x is 0, both conditions must be met simultaneously. First, consider 0x2F < x. After subtraction, how can we extract the sign bit? We can perform an arithmetic right shift by 31 bits so that the sign bit fills all 32 bits. That is, if 0x2F - x < 0, then (0x2F + (~x + 1)) >> 31 equals 0xFFFFFFFF, and if 0x2F - x >= 0, (0x2F + (~x + 1)) >> 31 equals 0; Next, consider x <= 0x39. Using the same method, if 0x39 - x < 0, then (0x39 + (~x + 1)) >> 31 equals 0xFFFFFFFF, and if 0x39 - x >= 0, (0x39 + (~x + 1)) >> 31 equals 0. We take the negation to satisfy this condition: Both conditions must be satisfied simultaneously, so: Since the final result is either 1 or 0, we extract the least significant bit: 
    1
    2
    3
    4
    5
    int isAsciiDigit(int x) {
      int low = (0x2F + (~x + 1)) >> 31;  // 0x2F - x < 0 => x > 0x2F (即 x >= 0x30)
      int high = ~((0x39 + (~x + 1)) >> 31);  // 0x39 - x >= 0 => x <= 0x39
      return low & high & 0x1;
    }

conditional

Problem:

1
2
3
4
5
6
7
8
9
10
/* 
 * conditional - same as x ? y : z 
 *   Example: conditional(2,4,5) = 4
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 16
 *   Rating: 3
 */
int conditional(int x, int y, int z) {
  return 2;
}

  • The expression for conditional is the same as x ? y : z.
  • To implement returning y or z based on the value of x using only bit operations is very difficult. Although it is easy to determine whether x is zero, it is hard to simultaneously associate x with both y and z. Therefore, we rely on addition operations and assume the return expression is: When x != 0, let a = -z = ~z + 1; When x == 0, let a = -y = ~y + 1 to satisfy the requirement. However, this is also difficult because a depends on both y and z, and a is determined by whether x is zero. Thus, we consider splitting a: When x is non-zero, let b = 0 and c = -z = ~z + 1; when x is zero, let b = -y = ~y + 1 and c = 0. This way, b depends only on y, and c depends only on z.
    First, we need to determine whether x is zero. This is straightforward using the NOT operation: when x is non-zero, it yields 0; when x is zero, it yields 1. Let’s focus on b. When !x == 0, b should be 0; when !x != 0, b should be ~z + 1. Clearly, the AND operation can achieve this: However, when !x != 0, !x equals 1, and its bitwise AND with ~z + 1 only preserves the least significant bit, which is not necessarily ~z + 1. Therefore, we need to ensure that when x != 0, the result is 0x. FFFFFFFF, and 0 when x == 0. Thus, we define a as: When x is zero, !x equals 1, and ~(!x) equals 0x. FFFFFFFE,a==0xFFFFFFFF；当x为非零时，!x==0，~(!x)==0xFFFFFFFFSince a == 0, the expression for b should be Next, consider c. The case for c is exactly the opposite of b, so simply add a ~ to a: There is no need to worry about addition overflow here.
1
2
3
4
5
6
int conditional(int x, int y, int z) {
  int a = ~(!x)+1;
  int b = a&(~y+1);
  int c = ~a&(~z+1);
  return b+y+c+z;
}

isLessOrEqual

Problem:

1
2
3
4
5
6
7
8
9
10
/* 
 * isLessOrEqual - if x <= y  then return 1, else return 0 
 *   Example: isLessOrEqual(4,5) = 1.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 24
 *   Rating: 3
 */
int isLessOrEqual(int x, int y) {
  return 2;
}

  • Return 1 if x <= y; otherwise, return 0.
  • To compare values using subtraction, compute y - x. If y - x >= 0 (sign bit is 0), return 1; if y - x < 0 (sign bit is 1), return 0. Since y - x = y + ~x + 1, right shift by 31 bits to extract the sign bit. We apply bitwise negation to ensure that when the sign bit is 0, the result is 1; when the sign bit is 1, the result is 0: 
1
2
3
int isLessOrEqual(int x, int y) {
  return ~((y+(~x+1))>>31) &0x1;
}

logicalNeg

Problem:

1
2
3
4
5
6
7
8
9
10
11
/* 
 * logicalNeg - implement the ! operator, using all of 
 *              the legal operators except !
 *   Examples: logicalNeg(3) = 0, logicalNeg(0) = 1
 *   Legal ops: ~ & ^ | + << >>
 *   Max ops: 12
 *   Rating: 4 
 */
int logicalNeg(int x) {
  return 2;
}

  • Implement the NOT operation: for !x, return 1 when x is 0, and return 0 when x is non-zero.
  • The most intuitive difference between 0 and non-zero values is that every bit of 0 is zero, while a non-zero value has at least one bit set to 1. However, since we cannot use looped shift operations to determine this, we must find an alternative approach.
  • Another distinguishing characteristic between 0 and non-zero values is that the negative of 0 is still 0, i.e., ~0 + 1 = 0, whereas the negative of a non-zero number is not 0. We can leverage this fact to check whether the negative of x equals x itself. Previously, we used a trick with XOR to check if two numbers are equal: this expression returns 0 when x is 0, and non-zero when x is non-zero, but this effectively does nothing. We can use another insight: the sign bit of a non-zero number and its negative must be opposite—one is 1, the other 0—while the sign bit of 0 and its negative are both 0. Therefore, by OR-ing the two, we get an expression whose sign bit is 1 when non-zero, and 0 when zero. Next, we extract the sign bit and invert it, because we want to return 1 when the input is 0, and 0 otherwise. We used this technique in the previous problem: perform an arithmetic right shift by 31 bits, invert the result, and then AND with 0x1 to isolate the least significant bit: 
1
2
3
int logicalNeg(int x) { 
   return ~(((~x+1)|x)>>31) & 0x1;
}

howManyBits

Problem:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/* howManyBits - return the minimum number of bits required to represent x in
 *             two's complement
 *  Examples: howManyBits(12) = 5
 *            howManyBits(298) = 10
 *            howManyBits(-5) = 4
 *            howManyBits(0)  = 1
 *            howManyBits(-1) = 1
 *            howManyBits(0x80000000) = 32
 *  Legal ops: ! ~ & ^ | + << >>
 *  Max ops: 90
 *  Rating: 4
 */
int howManyBits(int x) {
  return 0;
}

  • Return the number of bits required to represent x in binary two’s complement form. Essentially, this involves finding the position of the most significant 1 bit and then adding 1 bit for the sign bit. This problem is somewhat challenging and not very intuitive. Below is an implementation method from someone else.
  • Here, we use a binary search approach:
    First, consider positive numbers and zero.
  1. High 16 bits: Check if there is a 1 in the high 16 bits; if so, at least 16 bits are needed.
  2. High 8 bits: Within the remaining 16 bits, check if there is a 1 in the high 8 bits.
  3. High 4 bits: Within the remaining 8 bits, check if there is a 1 in the high 4 bits.
  4. High 2 bits: Within the remaining 4 bits, check if there is a 1 in the high 2 bits.
  5. High bit: Among the remaining 2 bits, check if the higher bit is 1.
  6. Least significant bit: The last remaining bit.
    Finally, sum the bit counts of all parts and add 1 for the sign bit.
  • Handling negative numbers:
    The flag is x >> 31, which is the sign bit. If x is negative, flag is 1; otherwise, it is 0.
  1. If x is negative (flag == 1), then x is bitwise inverted: x = ~x.
  2. If x is non-negative (flag == 0), x remains unchanged.
    In two’s complement representation of negative numbers, the sign bit and the value bits are combined. If you directly calculate the number of significant bits for a negative number, the sign bit will cause incorrect results. For example:
    The two’s complement of -1 is 11111111 11111111 11111111 11111111, if we directly count the bits, we get 32 bits, but in reality, we only care about the number of effective bits.
    By applying bitwise negation, the two’s complement representation of a negative number is converted into a positive number, and the number of effective bits in its binary form remains the same as that of the original negative number. For example:
  • The two’s complement of -1 is 11111111 11111111 11111111 11111111, and after negation it becomes 00000000 00000000 00000000 00000000, with an effective bit count of 1.
  • The two’s complement of -2 is 11111111 11111111 11111111 11111110, and after negation it becomes 00000000 00000000 00000000 00000001, with an effective bit count of 2.

howManyBits

https://zhuanlan.zhihu.com/p/559005736

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int howManyBits(int x) {
  int b16, b8, b4, b2, b1, b0;
  int flag = x >> 31;
  x = (flag & ~x) | (~flag & x);  // If the sign bit of x is 0, it remains unchanged; if the sign bit of x is 1, invert all bits
  
  b16 = !!(x >> 16) << 4;  // Check if the number is greater than or equal to 2^16
  x >>= b16;  
  b8 = !!(x >> 8) << 3;    // Check if the number is greater than or equal to 2^8
  x >>= b8;
  b4 = !!(x >> 4) << 2;    // Check if the number is greater than or equal to 2^4
  x >>= b4;
  b2 = !!(x >> 2) << 1;    // Check if the number is greater than or equal to 2^2
  x >>= b2;
  b1 = !!(x >> 1);         // Check if the number is greater than or equal to 2^1
  x >>= b1;
  b0 = x;                  // Check if the number is greater than or equal to 2^0
  
  return b0 + b1 + b2 + b4 + b8 + b16 + 1;  // Return the total number of bits required
}

floatScale2

Problem:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/* 
 * floatScale2 - Return bit-level equivalent of expression 2*f for
 *   floating point argument f.
 *   Both the argument and result are passed as unsigned int's, but
 *   they are to be interpreted as the bit-level representation of
 *   single-precision floating point values.
 *   When argument is NaN, return argument
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
 */
unsigned floatScale2(unsigned uf) {
  return 2;
}

  • Multiply a single-precision floating-point number (float) by 2, and return the binary representation of the result. The function’s input and output are both of type unsigned int, but they actually represent the binary bit pattern of a single-precision floating-point number. When the input is NaN, return it unchanged. Also, finally I get to use if and while😭😭😭

  • Let’s first review the concepts of IEEE 754 floating-point numbers:

Representation of IEEE 754

Single-precision float and double-precision double

There are three categories of floating-point numbers defined by IEEE 754:
Category 1: Normalized number

Denormalized numbers represent very small values close to zero, preventing floating-point underflow and ensuring the continuity of floating-point computations.
类别2：非规格化数

类别3：特殊值

IEEE 754 Representation Range

First, we extract the sign bit (sign), the fraction (frac), and the exponent (exp):



Based on the exponent, determine whether this floating-point number is normalized, denormalized, or one of the special cases.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
unsigned floatScale2(unsigned uf) { 
  unsigned exp = (uf & 0x7f800000) >> 23;
  unsigned sign = uf >> 31 & 0x1;
  unsigned frac = uf & 0x7FFFFF;
  
  if (exp == 0) {  // Denormalized number, exponent is 0, just multiply frac by 2
    frac <<= 1;
    return (sign << 31) | (exp << 23) | frac;
  } else if (exp == 0xFF) {  // Special case, NaN
    return uf;
  } else {
    exp++;  // Multiply by 2, equivalent to E + 1
    return (sign << 31) | (exp << 23) | frac;
  }
}

floatFloat2Int

Problem:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/* 
 * floatFloat2Int - Return bit-level equivalent of expression (int) f
 *   for floating point argument f.
 *   Argument is passed as unsigned int, but
 *   it is to be interpreted as the bit-level representation of a
 *   single-precision floating point value.
 *   Anything out of range (including NaN and infinity) should return
 *   0x80000000u.
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
 */
int floatFloat2Int(unsigned uf) {
  return 2;
}

  • Represent the input IEEE 754 floating-point number as an int; if it exceeds the representable range, return 0x8. 0000000u。
  • If it is a denormalized number, return 0 immediately; if it is a special case, return 0x8 immediately. 0000000u
  • If it is a normalized number, we first need to check whether it exceeds the int representation range. An int consists of 32 bits in total, with one bit for the sign bit. The maximum value is 2^31, and the minimum value is -(2^31 + 1). Therefore, the exponent E cannot exceed 30 (when E is 31, left shifting by E bits will overwrite the sign bit). When the exponent E is less than 0, it means the number is less than 1, so we directly return 0. Also:
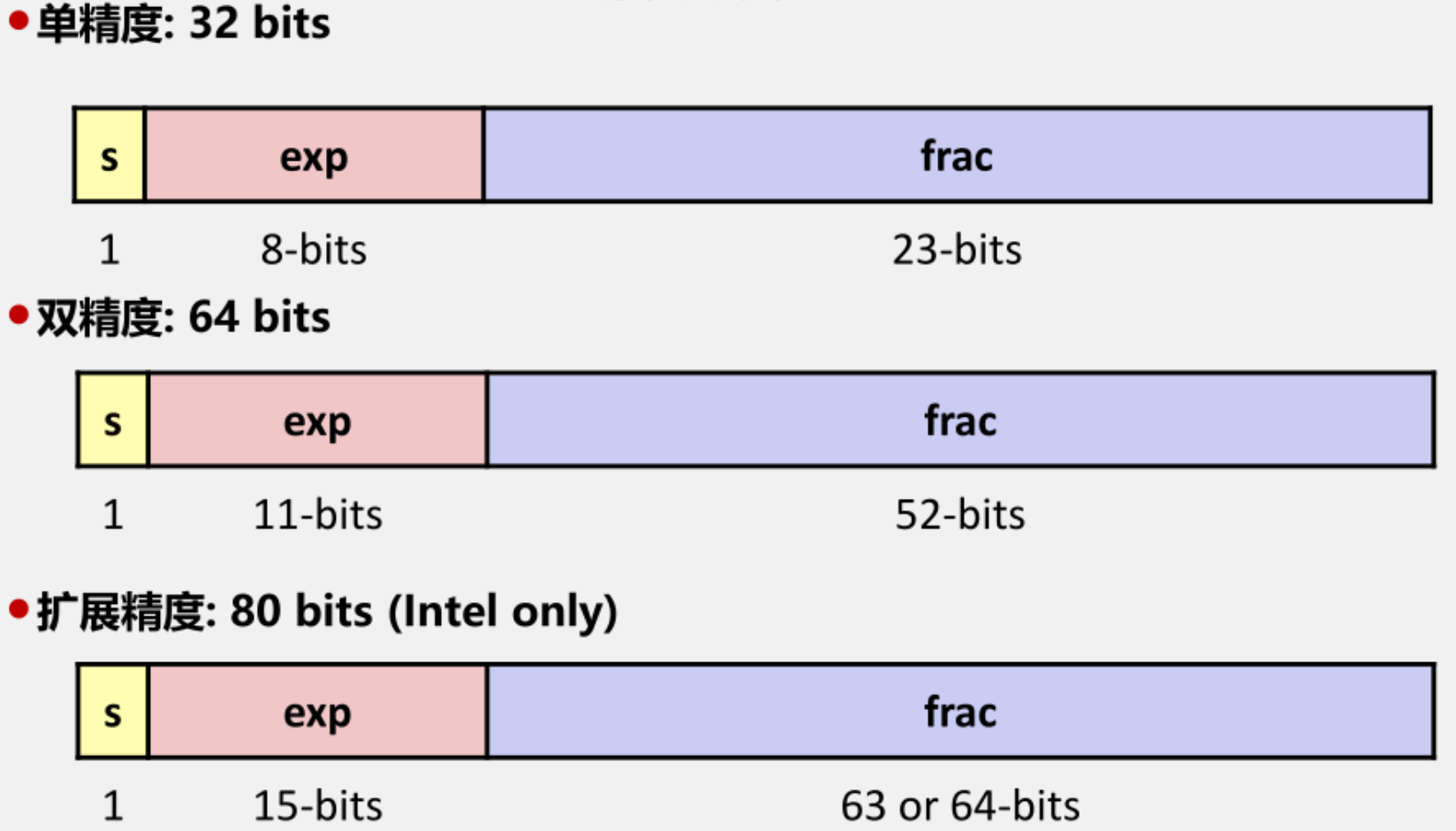
  • sign 1 bit
  • exp 8 bits
  • frac 23 bits

We can consider it as 1frac (the 24th bit is 1, and bits 1 to 23 form frac), which is equivalent to 1.frac (integer part 1, fractional part frac) left shifted by 23 bits. At this point, the exponent is E, meaning it should be multiplied by 2 to the power of E, i.e., left shifted by E bits. Therefore, when E is less than 23, we should right shift by (23 - E) bits to truncate the last (23 - E) bits of frac. When E is greater than 23, since this is equivalent to having already shifted left by 23 bits, you only need to shift left by (E - 23) additional bits.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
int floatFloat2Int(unsigned uf) {
  unsigned exp = (uf & 0x7f800000) >> 23;
  unsigned sign = uf >> 31 & 0x1;
  unsigned frac = uf & 0x7FFFFF;
  
  if (exp == 0xFF) {  // Special case
    return 0x80000000u;
  } else if (exp == 0) {  // Denormalized number
    return 0x0;
  } else {                   // Normalized number
    int E = exp - 127;  // Exponent, note not to set as unsigned
    if (E >= 31) {           // Out of range
      return 0x80000000u;
    } else if (E < 0) {  // If E < 0, it means the number is smaller than 1, return 0
      return 0;
    }
    frac = frac | (1 << 23);  // Set the implicit 1 in the fraction
    if (E < 23) {
      frac = frac >> (23 - E);
    } else {
      frac = frac << (E - 23);
    }
    if (sign == 0) {  // Return positive or negative based on the sign bit
      return frac;
    } else {
      return -frac;
    }
  }
}

floatPower2

Problem:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/* 
 * floatPower2 - Return bit-level equivalent of the expression 2.0^x
 *   (2.0 raised to the power x) for any 32-bit integer x.
 *
 *   The unsigned value that is returned should have the identical bit
 *   representation as the single-precision floating-point number 2.0^x.
 *   If the result is too small to be represented as a denorm, return
 *   0. If too large, return +INF.
 * 
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. Also if, while 
 *   Max ops: 30 
 *   Rating: 4
 */
unsigned floatPower2(int x) {
    return 2;
}

  • Calculate 2.0^x and return its unsigned representation according to IEEE 754. If the result is too small—so small that even denormalized numbers cannot represent it—return 0. If the result is too large, return +INF. Clearly, this problem primarily tests the representable range of IEEE 754.

For float single precision

  • Sign bit sign: 1 bit
  • Exponent exp: 8 bits
  • Fraction frac: 23 bits

Representable range

  • Normalized numbers: The exponent exp is neither all zeros nor all ones,
    $
    V = (-1)^S \times 2^E \times M = (-1)^{sign} \times 2^{exp - bias} \times (1 + frac)
    $
    The exponent ranges from 1 to 254, with E = Exp - Bias = Exp - 127, so E ranges from -126 to 127. For frac, the minimum value is 0 and the maximum is 1 - 2^{-23}. Therefore, ignoring S,
    $
    V{max} = (-1)^S \times 2^{127} \times (2 - 2^{-23}) = (-1)^S \times 2^{127} \times (2 - 2^{-23})
    $
    $
    V    {min} = (-1)^S \times 2^{-126} \times (1 + 0) = (-1)^S \times 2^{-126}
    $

  • Denormalized number: exponent all zeros
    $
    V = (-1)^S \times 2^E \times M = (-1)^{sign} \times 2^{1 - Bias} \times (0 + frac)
    $
    The exponent exp is all zeros, so E = 1 - Bias = 1 - 127 = -126. Therefore:
    $
    V = (-1)^{sign} \times 2^{-126} \times (0 + frac)
    $
    For frac, the minimum value is 0, but the smallest representable nonzero value is 2^{-23}. Values between 0 and 2^{-23} cannot be represented. The maximum value is 1 - 2^{-23}. Thus, when frac is 0, the value is 0. However, to calculate the smallest representable nonzero value, frac must be set to 2^{-23}, ignoring S:
    $
    V{max} = (-1)^S \times 2^{-126} \times (0 + 1 - 2^{-23}) = (-1)^S \times 2^{-126} \times (1 - 2^{-23})
    $
    $
    V    {min} = (-1)^S \times 2^{-126} \times (0 + 2^{-23}) = (-1)^S \times 2^{-149}
    $

    • Special values
  1. +infinity: all bits of exp are 1, frac is 0, and S is 0
  2. -infinity: all bits of exp are 1, frac is 0, and S is 1
  3. NaN: all bits of exp are 1, and frac is not 0

Therefore, based on the above analysis:

  • Return +NaN when x > 127
  • A normalized number when -126 ≤ x ≤ 127
  • Denormalized number when -149 ≤ x < -126
  • Return 0 when x < -149 because the value is too small to represent
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    unsigned floatPower2(int x) {
      if (x > 127) {  // Return +infinity, S=0, exp=0xFF, frac=0;
        return 0xFF << 23;
      } else if (-126 <= x && x <= 127) {  // Normalized number, exp = E + Bias = E + 127
        return (x + 127) << 23;
      } else if (-149 <= x && x < -126) {  // Denormalized number, exp=0, E = 1 - Bias = -126, 2^(-126) * frac
        return 1 << (23 - (-x - 126));  // E already has 2^(-126), when frac is 0x1, it represents 2^(-23), assuming input x is -127, frac should be 2^(-1), i.e., 1 shifted left by 22 bits
      } else {  // x < -149, too small, return 0
        return 0;
      }
    }