时间轴

2025-03-07

写到howManyBits

2025-03-07

写完了，再一次感觉这个实验不错

最近担任计算机系统助教要验收这个CSAPP的实验，这个实验本科的时候就做过，但过了这么久基本忘完了，遂重新做一遍记录于此。

实验环境搭建

我是在win10 WSL2环境下做的：

实验环境

具体如何搭建环境参考下面这个链接，有脚本一键搭建运行环境，非常方便：

CSAPP环境搭建

https://zhuanlan.zhihu.com/p/505497911

简介

在bits.c中完成函数实现，但对代码有一定的限制

1
2
3
4
5
6
# 检测代码是否符合要求的规范
./dlc bits.c
# 查看分数
make clean 
make 
./btest

实验内容

bitXor

题目：

1
2
3
4
5
6
7
8
9
10
/* 
 * bitXor - x^y using only ~ and & 
 *   Example: bitXor(4, 5) = 1
 *   Legal ops: ~ &
 *   Max ops: 14
 *   Rating: 1
 */
int bitXor(int x, int y) { 
  return 2;
}

要求只用~(按位取反)和&(按位与)实现异或，可以使用离散数学中的等值演算，异或即“相同为0，不同为1”：

$$
x \oplus y = \lnot (\lnot x \land \lnot y) \land \lnot ( x \land y)
$$

1
2
3
int bitXor(int x, int y) { 
  return ( ~(~x & ~y)) & (~(x & y));
}

tmin

题目：

1
2
3
4
5
6
7
8
9
/* 
 * tmin - return minimum two's complement integer 
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 4
 *   Rating: 1
 */
int tmin(void) {
  return 2;
}

返回最小的二进制补码整数，关于原码，反码，补码定义如下：

表示方法 定义
原码 最高位为符号位（0 表示正数，1 表示负数），其余位表示数值的绝对值
反码 正数的反码与原码相同；负数的反码是符号位不变，其余位按位取反
补码 正数的补码与原码相同；负数的补码是其反码加 1

补码的编码具有不对称性，除了最小的负数其他负数都其正数与之对应，在 64 位系统中，整数的补码表示范围是：

  • 最小负数：0x8000000000000000（即 -2^63）。
  • 最大正数：0x7FFFFFFFFFFFFFFF（即 2^63 - 1）
1
2
3
int tmin(void) {
  return 1 << 31;
}

isTmax

题目：

1
2
3
4
5
6
7
8
9
10
/*
 * isTmax - returns 1 if x is the maximum, two's complement number,
 *     and 0 otherwise 
 *   Legal ops: ! ~ & ^ | +
 *   Max ops: 10
 *   Rating: 1
 */
int isTmax(int x) {
  return 2;
}
  • 如果x是二进制补码最大值则返回1,否则返回0。
  • 最大值是0x7FFFFFFF，它的特点是最高位为0其余为1，那么0x7FFFFFFF+0x1后变为0x800000000，最高位为1其余为0，其特点正好相反。
  • 这里需要用到异或的特性，如x^target，x取反后与target异或，由于异或是不同为1相同为0，则只有当x与target完全相同时，x^target才会为0x0，那么加上!操作符就能得到!(x^target)即x与target相同时为1,不同时为0。
    对于0x7FFFFFFF，它加1后为0x80000000，由于特点正好相反，取反后有变为0x7FFFFFFF,故可以利用异或判断是否相同即：!(~(x+1)^x) 。
  • 继续思考，是不是只有0x7FFFFFFF才满足这样的特性：+1后相当于按位取反？显然0xFFFFFFFF也满足这个特性，这是因为溢出时最高位被丢弃变为0x0。所以我们还需要构造一个表达式与!((x+1)^x) 相与记为expression1，即!((x+1)^x) & expression1。当x为0x7FFFFFFF时expression1为1，当x为0xFFFFFFFF时为0。
  • 排除的方法必定需要利用0x7FFFFFFF有而0xFFFFFFFF没有的特点0，即这两个数的区别，而最简单的区别就是0x7FFFFFFF+0x1后变为0x8FFFFFFF是个非零数，而0xFFFFFFFF+0x1后变为0。故!(x+1)在x为0x7FFFFFFF时为0，在x为0xFFFFFFFF时为1，!(x+1)与需要的正好相反，再加上一个!运算即可，即：
1
2
3
int isTmax(int x) {
  return !( ~(x + 1) ^ x) & !!(x + 1);
}

allOddBits

题目：

1
2
3
4
5
6
7
8
9
10
11
/* 
 * allOddBits - return 1 if all odd-numbered bits in word set to 1
 *   where bits are numbered from 0 (least significant) to 31 (most significant)
 *   Examples allOddBits(0xFFFFFFFD) = 0, allOddBits(0xAAAAAAAA) = 1
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 12
 *   Rating: 2
 */
int allOddBits(int x) {
  return 2;
}
  • 如果所有奇数位的比特位是1返回1，否则返回0，即一个数只要其1,3,5,7…位为1（其余位不用管）返回1，否则返回0。
  • 我们可以去除所有的偶数位的影响，看奇数位，比如让x与0xAAAAAAAA相与，则所有的偶数位都为0，再看其是否和0xAAAAAAAA相同（利用isTmax中阐述的通过按位与判断两个数是否相同）。也可以让x与0x55555555相或，则所有的偶数位为1，再看其是否和0xFFFFFFFF相同。即：
  • 但是由于实验要求的限制条件，不只直接写0xAAAAAAAA这种，只能写0xAA，通过位运算得到0xAAAAAAAA

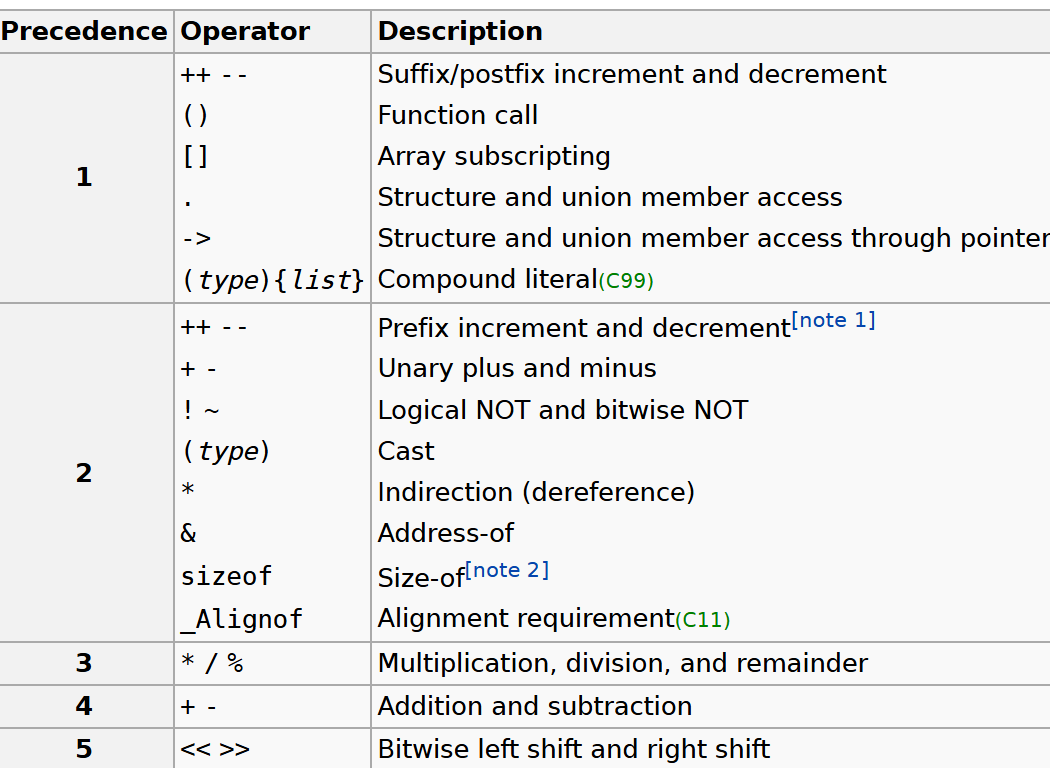
注意：根据C规范移位运算优先级低于加减

https://en.cppreference.com/w/c/language/operator_precedence

1
2
3
4
5
6
7
8
int allOddBits(int x) {
  // return !((x|0x55555555)^0xFFFFFFFF);
  // return !((x&0xAAAAAAAA)^(0xAAAAAAAA));
  int a = 0xAA<<8;//0x00AA
  int b = a | 0xAA;//0xAAAA
  int c = b<<16 | b;//0xAAAAAAAA
  return !((x&c)^c);
}

negate

题目：

1
2
3
4
5
6
7
8
9
10
/* 
 * negate - return -x 
 *   Example: negate(1) = -1.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 5
 *   Rating: 2
 */
int negate(int x) { 
  return 2;
}
  • 返回x的负数
  • 我们知道：
  • 两式子相减得到：
1
2
3
int negate(int x) { 
  return ~x+1;
}

isAsciiDigit

题目：

1
2
3
4
5
6
7
8
9
10
11
12
/* 
 * isAsciiDigit - return 1 if 0x30 <= x <= 0x39 (ASCII codes for characters '0' to '9')
 *   Example: isAsciiDigit(0x35) = 1.
 *            isAsciiDigit(0x3a) = 0.
 *            isAsciiDigit(0x05) = 0.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 15
 *   Rating: 3
 */
int isAsciiDigit(int x) {
  return 2;
}
  • 检测x是否属于ascii的数字，简单来说是判断x是否在0x30和0x39之间。
  • 在汇编中判断大小是通过减法置标志位来完成的，因此我们可以通过让0x30和0x39分别减去x再取符号位，看是否满足：0x30-x应该小于0符号位为1，0x39-x>0符号位为0，但是若是x落在边界时,如x==0x30，0x30-x为0符号位为0也是满足要求的，因此我们可以把<=变为<：

上式等价于：

那么右边x<0x39是否需要等价转换?0x39-x应该大于或等于0，符号位为0，0x39-x<0符号位为1，经分析边界条件是囊括的所以不需要等价转换（转换后会把边界条件排出）。
让0x2F-x符号位为1，0x39-x符号位为0，必须同时满足这两个条件，首先先看0x2F< x，相减后如何提取符号位？可以通过算数右移，移动31位符号位占满整个32位，即若0x2F-x<0，则(0x2F+(x+1))>>31为0xFFFFFFFF，若0x2F-x>=0,(0x2F+(x+1))>>31为0;

再看x <= 0x39，同样的方法，若0x39-x<0，则(0x39+(x+1))>>31为0xFFFFFFFF，若0x39-x>=0,(0x39+(x+1))>>31为0;我们取个反就可以满足

需要同时满足上述两个条件，故

由于最后返回1或0，我们取最低位即可：

1
2
3
4
5
int isAsciiDigit(int x) {
  int low = (0x2F + (~x + 1)) >> 31;  // 0x2F - x < 0 => x > 0x2F (即 x >= 0x30)
  int high = ~((0x39 + (~x + 1)) >> 31);  // 0x39 - x >= 0 => x <= 0x39
  return low & high & 0x1;
}

conditional

题目：

1
2
3
4
5
6
7
8
9
10
/* 
 * conditional - same as x ? y : z 
 *   Example: conditional(2,4,5) = 4
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 16
 *   Rating: 3
 */
int conditional(int x, int y, int z) {
  return 2;
}
  • conditional的表达式和 x ? y : z 相同
  • 要实现这种根据x的值判断返回y还是返回z，仅仅使用位运算非常难，因为虽然我们很容易判断x是否为0，但我们很难将x与yz同时关联起来，所以我们把希望留给加法运算，假设返回这样的式子：

当x!=0时，让a=-z=z+1；当x==0时，让a=-y=y+1就可以满足要求，但是这个要求同样难以满足，因为a既与y有关又与z有关，而a又由x是否为0来决定，因此我们考虑将a拆分：

当x为非0时，让b=0，c=-z=z+1；当x为0时，让b=-y=y+1，c=0。这样可以让b只与y有关，c只与z有关。
首先我们要判断x是否为0，这个不难，使用!运算即可，当x为非零则为0，当x为0则为1，我们首先关注b，!x==0时，b要为0，!x!=0时，b要为~z+1，显然与运算可以满足：

但是当!x!=0时，!x==1，而它与z+1按位与只会留下最低位不一定是z+1，因此我们需要让x!=0时得到0xFFFFFFFF，x==0时得到0，因此我们定义a：

当x为0时,!x==1,(!x)==0xFFFFFFFE,a==0xFFFFFFFF；当x为非零时，!x==0，(!x)==0xFFFFFFFF，a==0，因此b的表达式应为

再关注c，c的情况刚好与b相反，那么只需要给a再加一个~即可

这里不用担心加法溢出问题

1
2
3
4
5
6
int conditional(int x, int y, int z) {
  int a = ~(!x)+1;
  int b = a&(~y+1);
  int c = ~a&(~z+1);
  return b+y+c+z;
}

isLessOrEqual

题目：

1
2
3
4
5
6
7
8
9
10
/* 
 * isLessOrEqual - if x <= y  then return 1, else return 0 
 *   Example: isLessOrEqual(4,5) = 1.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 24
 *   Rating: 3
 */
int isLessOrEqual(int x, int y) {
  return 2;
}
  • 如果x<=y那么返回 1，否则返回0
  • 比大小利用减法，让y-x如果y-x>=0即符号位为0则返回1，如果y-x<0即符号位为1则返回0，y-x=y+~x+1，然后右移31位后取符号位,我们需要一个取反操作以满足符号位为0返回1，符号位为1则返回0:
1
2
3
int isLessOrEqual(int x, int y) {
  return ~((y+(~x+1))>>31) &0x1;
}

logicalNeg

题目：

1
2
3
4
5
6
7
8
9
10
11
/* 
 * logicalNeg - implement the ! operator, using all of 
 *              the legal operators except !
 *   Examples: logicalNeg(3) = 0, logicalNeg(0) = 1
 *   Legal ops: ~ & ^ | + << >>
 *   Max ops: 12
 *   Rating: 4 
 */
int logicalNeg(int x) {
  return 2;
}
  • 实现!运算符，即对于!x，当x为0时返回1，当x为非0时返回0
  • 0和非零最直观的区别就在与0的每一位都是0，而非零至少有一位为1，但因为我们无法利用循环移位操作来判断，故只能另辟蹊径
  • 0的和非零的另一个不同特点在于0的负数还是0，即~0+1=0，而非零数的负数不是0，我们可以利用这点，看x的负数是否与它自己相同，前面我们用到过一个技巧通过异或来判断两数是否相同：这个表达式在x等于0时返回0，x等于非零时返回非零，但是这样等于没做

我们可以利用另一点，非零数的负数和原来这个数的符号位肯定相反，一个必是1，一个必是0，而0的负数的符号位和0的符号位都是0，因此我们只需要将两者相与就能得到：非零时该表达式符号位为1，为0时该表达式符号位0

接下来就是提取符号位了，顺便取个反，因为我们要求为0时返回1，为1时返回0，这个技巧我们在上面的题目用到过：即将其向右算数移位31位并取反，然后与0x1相与取最低位：

1
2
3
int logicalNeg(int x) { 
   return ~(((~x+1)|x)>>31) & 0x1;
}

howManyBits

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/* howManyBits - return the minimum number of bits required to represent x in
 *             two's complement
 *  Examples: howManyBits(12) = 5
 *            howManyBits(298) = 10
 *            howManyBits(-5) = 4
 *            howManyBits(0)  = 1
 *            howManyBits(-1) = 1
 *            howManyBits(0x80000000) = 32
 *  Legal ops: ! ~ & ^ | + << >>
 *  Max ops: 90
 *  Rating: 4
 */
int howManyBits(int x) {
  return 0;
}
  • 返回以二进制补码的形式表示x需要几个比特数，其实就是看这个数的最高位1在第几位，然后加上1位符号位，这个问题有点难度，主要是有点难想到，下面是别人的实现方法。
  • 这里用到二分法：
    先考虑正数和0
  1. 高 16 位：检查高 16 位是否有 1，如果有，则至少需要 16 位。
  2. 高 8 位：在剩下的 16 位中，检查高 8 位是否有 1。
  3. 高 4 位：在剩下的 8 位中，检查高 4 位是否有 1。
  4. 高 2 位：在剩下的 4 位中，检查高 2 位是否有 1。
  5. 高 1 位：在剩下的 2 位中，检查高 1 位是否有 1。
  6. 最低位：最后剩下的 1 位。
    最终，将所有部分的位数相加，并加 1（符号位）。
  • 对负数的处理：
    flag 是 x >> 31，即符号位。如果 x 是负数，flag 为 1；否则为 0。
  1. 如果 x 是负数（flag == 1），则 x 被取反：x = ~x。
  2. 如果 x 是非负数（flag == 0），则 x 保持不变。
    负数的补码表示中，符号位和数值部分是混合在一起的。如果直接计算负数的有效位数，符号位会导致结果错误。例如：
    -1 的补码是 11111111 11111111 11111111 11111111，如果直接计算位数，会得到 32 位，但实际上我们只关心其有效位数。
    通过取反操作，负数的补码表示会被转换为正数，其二进制表示中的有效位数与原来的负数相同。例如：
  • -1 的补码是 11111111 11111111 11111111 11111111，取反后为 00000000 00000000 00000000 00000000，有效位数为 1。
  • -2 的补码是 11111111 11111111 11111111 11111110，取反后为 00000000 00000000 00000000 00000001，有效位数为 2。

howManyBits

https://zhuanlan.zhihu.com/p/559005736

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int howManyBits(int x) {
  int b16, b8, b4, b2, b1, b0;
  int flag = x >> 31;
  x = (flag & ~x) | (~flag & x);  // x符号位为0不变 ,x符号位为1按位取反
  b16 = !!(x >> 16) << 4; 
  x >>= b16;  
  b8 = !!(x >> 8) << 3;
  x >>= b8;
  b4 = !!(x >> 4) << 2;
  x >>= b4;
  b2 = !!(x >> 2) << 1;
  x >>= b2;
  b1 = !!(x >> 1);
  x >>= b1;
  b0 = x;
  return b0 + b1 + b2 + b4 + b8 + b16 + 1;
}

floatScale2

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/* 
 * floatScale2 - Return bit-level equivalent of expression 2*f for
 *   floating point argument f.
 *   Both the argument and result are passed as unsigned int's, but
 *   they are to be interpreted as the bit-level representation of
 *   single-precision floating point values.
 *   When argument is NaN, return argument
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
 */
unsigned floatScale2(unsigned uf) {
  return 2;
}

  • 将一个单精度浮点数（float）乘以 2，并返回结果的二进制表示。函数的输入和输出都是 unsigned int 类型，但它们实际上表示的是单精度浮点数的二进制位模式，当输入是NaN时返回这个输入即可，另外，终于可以用if while了😭😭😭

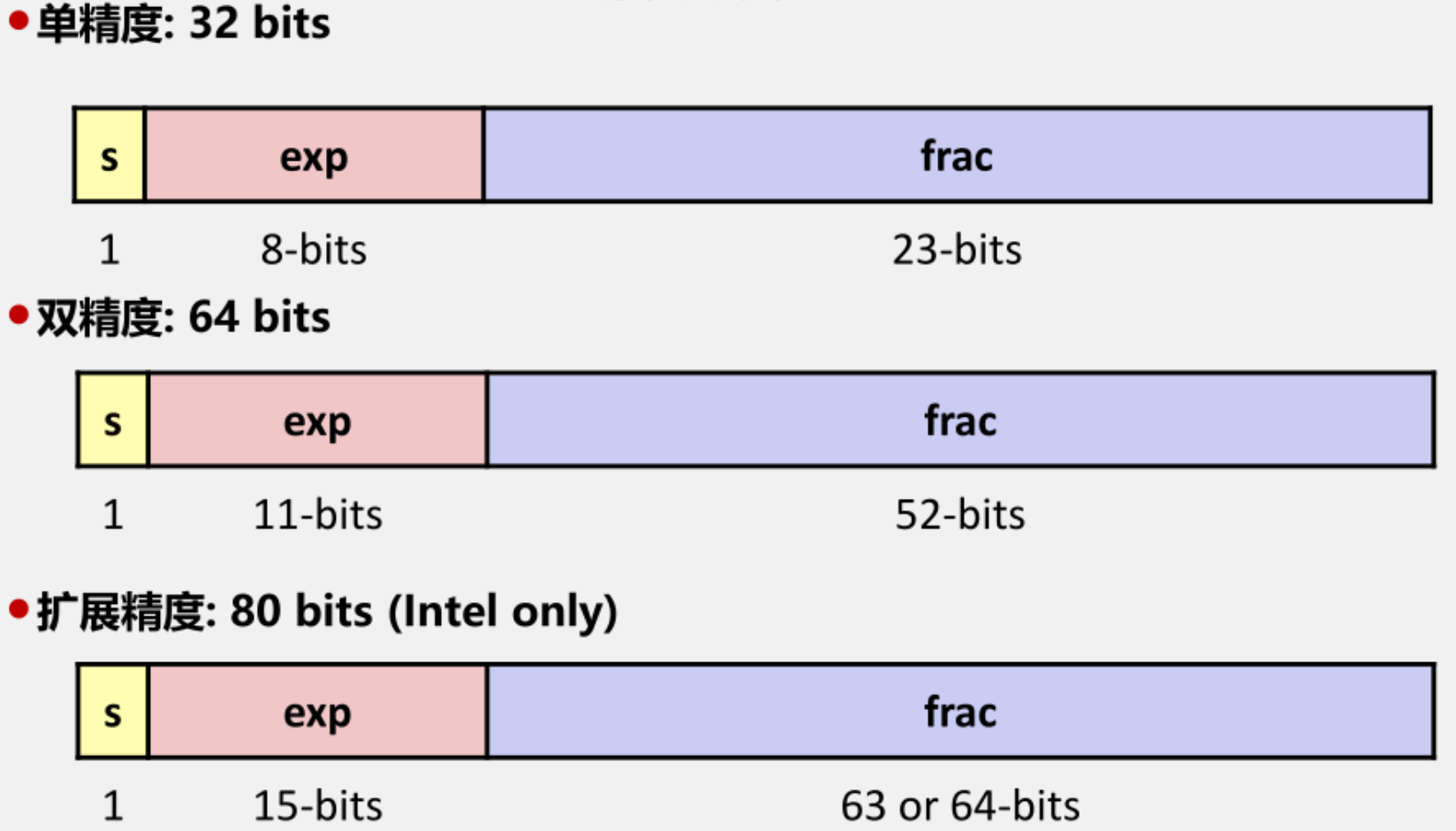
  • 先回顾下IEEE 754浮点数的知识：

IEEE 754的表示形式

单精度float 双精度double

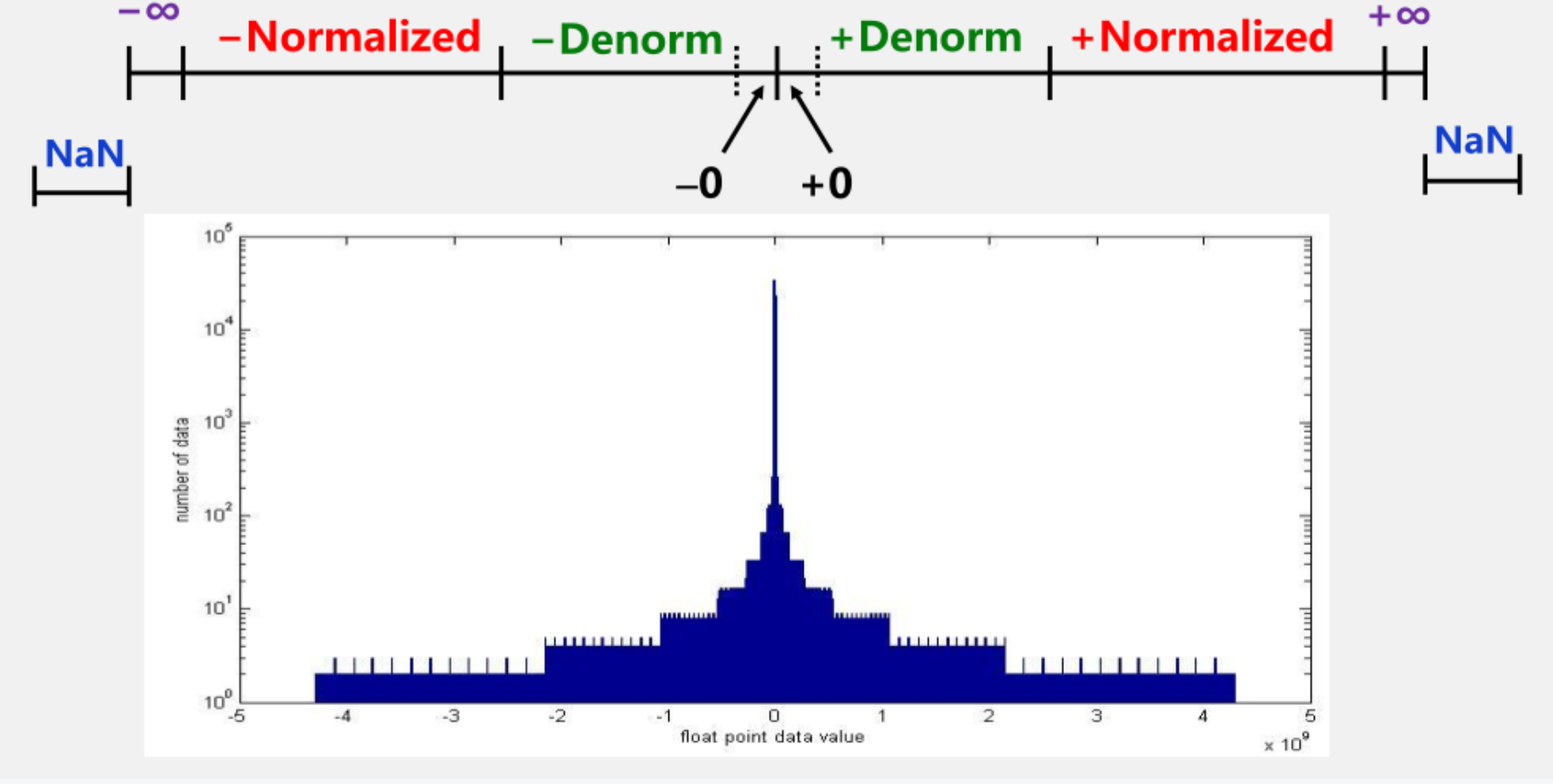
对于IEEE 754表示的浮点数，一共有三种类别
类别1：规格化数

非规格化数用于表示接近零的极小数值，防止浮点下溢（Underflow），保证浮点运算的连续性。
类别2：非规格化数

类别3：特殊值

IEEE 754 表示范围

首先我们先提取符号位sign，尾数frac，阶码exp：

根据阶码判断这个浮点数是规格化数，非规格化数还是特殊情况中的哪一种

1
2
3
4
5
6
7
8
9
10
11
12
13
14
unsigned floatScale2(unsigned uf) { 
  unsigned exp = (uf&0x7f800000)>>23;
  unsigned sign=uf>>31&0x1;
  unsigned frac=uf&0x7FFFFF;
  if(exp == 0){//非规格化数，阶码为0，直接让frac乘以2即可
    frac <<= 1;
    return (sign << 31) | (exp << 23) | frac;
  }else if(exp==0xFF){//特殊情况，非数
    return uf;
  }else{
    exp++;//乘2,相当于E+1,相当于
    return (sign << 31) | (exp << 23) | frac;
  }
}

floatFloat2Int

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/* 
 * floatFloat2Int - Return bit-level equivalent of expression (int) f
 *   for floating point argument f.
 *   Argument is passed as unsigned int, but
 *   it is to be interpreted as the bit-level representation of a
 *   single-precision floating point value.
 *   Anything out of range (including NaN and infinity) should return
 *   0x80000000u.
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
 */
int floatFloat2Int(unsigned uf) {
  return 2;
}
  • 用int表示输入的IEEE 754浮点数，如果超过表示范围则返回0x80000000u。
  • 如果是非规格化数，直接返回0，如果是特殊情况直接返回0x80000000u
  • 如果是规格化数，我们需要先判断是否超出int表示范围，int一共32位，一位表示符号位，最大表示2^31，最小表示-(2^31+1)，因此阶码E不能超过30（当E为31时左移E位会覆盖符号位）；当阶码E小于0时，说明是个小于1的数，直接返回0；又：
  • sign 1位
  • exp 8位
  • frac 23位

$$
V = (-1)^{sign} \times 2^{exp - 127} \times (1 + frac)
$$

我们可以可以看成1frac（第24位为1，第1~23位构成frac）而此时相当于由1.frac（整数部分位1，小数部分为frac）左移了23位，此时阶码为E，即要乘以E个2，也就是左移E位，所以，当E小于23时，应该右移（23-E）位以截断frac后面的(23-E)位；当E大于23时，由于此时相当于已经左移了23位，所以只需再左移(E-23)位。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
int floatFloat2Int(unsigned uf) {
 unsigned exp = (uf & 0x7f800000) >> 23;
  unsigned sign = uf >> 31 & 0x1;
  unsigned frac = uf & 0x7FFFFF;
  if (exp == 0xFF) {  // 特殊情况
    return 0x80000000u;
  } else if (exp == 0) {  // 非规格化数
    return 0x0;
  } else {                   // 规格化数
    int E = exp - 127;  // 阶码，注意不要设置为unsigned
    if (E >= 31) {           // 超范围
      return 0x80000000u;
    }else if(E<0){//如果E<0说明是个比1小的数，返回0
      return 0;
    }
    frac = frac | (1 << 23);  // 填上frac的1
    if (E < 23) {
      frac = frac >> (23 - E);
    } else {
      frac = frac << (E - 23);
    }
    if (sign == 0) {//根据符号位返回正负
      return frac;
    } else {
      return -frac;
    }
  }
}

floatPower2

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/* 
 * floatPower2 - Return bit-level equivalent of the expression 2.0^x
 *   (2.0 raised to the power x) for any 32-bit integer x.
 *
 *   The unsigned value that is returned should have the identical bit
 *   representation as the single-precision floating-point number 2.0^x.
 *   If the result is too small to be represented as a denorm, return
 *   0. If too large, return +INF.
 * 
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. Also if, while 
 *   Max ops: 30 
 *   Rating: 4
 */
unsigned floatPower2(int x) {
    return 2;
}
  • 计算2.0^x，并返回IEEE 754下的unsigned表示，如果结果太小，小到非规格化数都不能表示则返回0，如果结果太大返回+INF，很明显这题主要考察IEEE 754的表示范围。

对于float单精度

  • 符号位sign：1位
  • 阶码exp: 8位
  • 尾数frac：23位

表示范围

  • 规格化数：阶码exp既不全为0，也不全为1，
    $$
    V = (-1)^S \times 2^E \times M = (-1)^{sign} \times 2^{exp - bias} \times (1 + frac)
    $$
    exp范围为1~254,E=Exp-Bias=Exp-127，E的范围为-126>=E>=127;而对于frac，最小值为0，最大值为1-2^(-23),因此，不考虑S的情况下
    $$
    V_{max} = (-1)^S \times 2^{127} \times (2-2^{-23}) = (-1)^S \times 2^{127} \times (2-2^{-23})
    $$
    $$
    V_{min} = (-1)^S \times 2^{-126} \times (1+0) = (-1)^S \times 2^{-126}
    $$

  • 非规格化数：阶码全为0
    $$
    V = (-1)^S \times 2^E \times M = (-1)^{sign} \times 2^{1-Bias} \times (0 + frac)
    $$
    阶码exp全为0,E=1-Bias=1-127=-126，因此：
    $$
    V = (-1)^{sign} \times 2^{- 126} \times (0 + frac)
    $$
    对于frac来说，最小值为0，但能表示的最小非零是2^(-23),0~2^(-23)无法表示,最大值为1-2^(-23)，因此，当frac取0时，值为0，但要计算表示的最小非零时要令frac=2^(-23)，在不考虑S的情况下
    $$
    V_{max} = (-1)^S \times 2^{-126} \times (0+1-2^{-23}) = (-1)^S \times 2^{-126} \times (1-2^{-23})
    $$
    $$
    V_{min} = (-1)^S \times 2^{-126} \times (0+2^{-23}) = (-1)^S \times 2^{-149}
    $$

  • 特殊值

  1. +infinity：exp所有位全为1，frac为0，S为0
  2. -infinity：exp所有位全为1，frac为0，S为1
  3. NaN：exp所有位全为1，frac不为0

因此，经上述分析:

  • 当x>127时返回+NaN
  • 当-126<=x<=127时为规格化数
  • 当 -149 <= x < -126时为非规格化数
  • 当 x < -149时，太小了无法表示返回0
1
2
3
4
5
6
7
8
9
10
11
unsigned floatPower2(int x) {
  if (x > 127) {  // 返回+infinity,S=0,exp=0xFF,frac=0;
    return 0xFF << 23;
  } else if (-126 <= x && x <= 127) {  // 规格化数,exp=E+Bias=E+127
    return (x + 127) << 23;
  } else if (-149 <= x && x < -126) {  // 非规格化数,exp=0,E=1-Bias=-126,2^(-126)*frac
    return 1<<(23-(-x-126));//E已经有了2^(-126),当frac为0x1时表示2^(-23),假设输入x为-127,则frac要为2^(-1),即1向左移动22位
  } else {//x< -149,太小了返回0
    return 0;
  }
}