leetcode每日一题 P2536 子矩阵元素加 1

---

时间轴

2025-11-14

init

---

题目：

P2536 子矩阵元素加 1

https://leetcode.cn/problems/increment-submatrices-by-one/description/?envType=daily-question&envId=2025-11-14

差分矩阵的模板问题，可以推广到子矩阵加其他整数，不局限于+1。对差分矩阵O(1)操作就可以留下子矩阵+1的痕迹，然后根据前缀和与差分互为逆运算的性质，再对差分矩阵求前缀和就能得到答案。

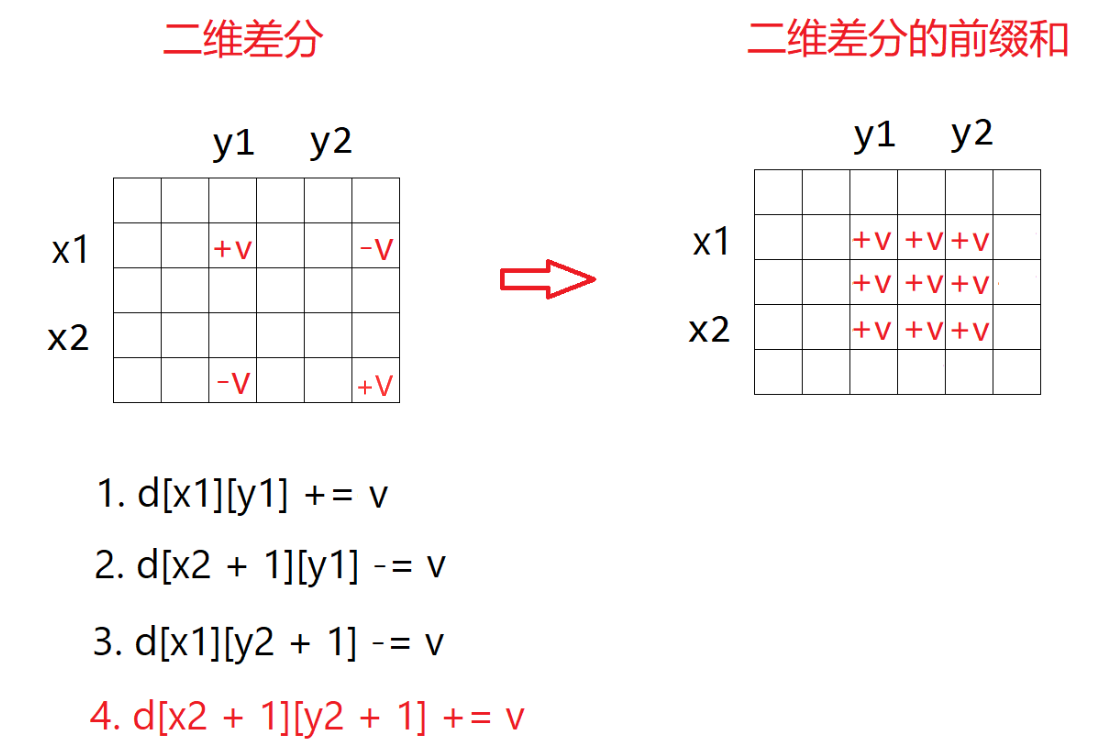
二维差分的前缀和是指从(0,0)到(i,j)的矩阵的和

注意差分矩阵的大小！要比原矩阵大1圈

#include <vector>
using std::vector;

class Solution {
    public:
	vector<vector<int> > rangeAddQueries(int n, vector<vector<int> > &queries)
	{
		vector<vector<int> > mat(n, vector<int>(n, 0));
		// 差分矩阵
		vector<vector<int> > diff(n + 1, vector<int>(n + 1, 0));
		int row1, col1, row2, col2;
		int x1, x2, x3;
		for (const auto &query : queries) {
			row1 = query[0];
			col1 = query[1];
			row2 = query[2];
			col2 = query[3];
			diff[row1][col1] += 1;
			diff[row2 + 1][col1] -= 1;
			diff[row1][col2 + 1] -= 1;
			diff[row2 + 1][col2 + 1] += 1;
		}

		// 前缀和+差分
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < n; j++) {
				x1 = i >= 1 ? mat[i - 1][j] : 0;
				x2 = j >= 1 ? mat[i][j - 1] : 0;
				x3 = i >= 1 && j >= 1 ? mat[i - 1][j - 1] : 0;
				mat[i][j] = diff[i][j] + x1 + x2 - x3;
			}
		}
		return mat;
	}
};