时间轴

2025-11-09

add 滑动窗口，回溯，动态规划

2025-11-27

update 滑动窗口，回溯

2025-12-05

add heap sort, quick sort

双指针

快慢指针

左右指针

滑动窗口

经典模板

1
2
3
4
5
6
7
8
9
int left=0, right=0;
while(right < s.size()){
    windows.add(s[right]);
    right++;
    while(windows需要收缩){
        windows.remove(s[left]);
        left++;
    }
}

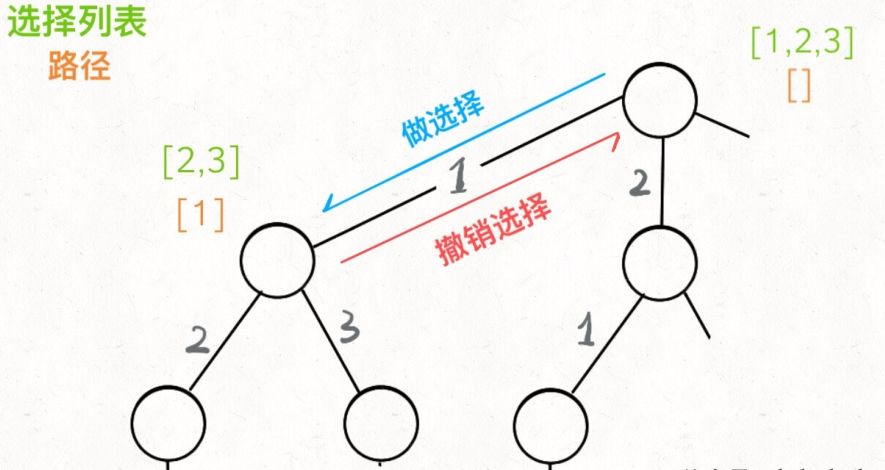
回溯

解决⼀个回溯问题，实际上就是⼀个决策树的遍历过程。

1,2,3的全排列

你只需要思考个问题：

  1. 路径：也就是已经做出的选择。
  2. 选择列表：也就是你当前可以做的选择。
  3. 结束条件：也就是到达决策树底层，⽆法再做选择的条件。

经典模板框架

1
2
3
4
5
6
7
8
9
10
11
12
result = []
void backtrace(路径，选择列表){
    if (满足结束条件){
        result.add(路径)
        return;
    }
    for(选择&: 选择列表){
        做选择,当前选择加入选择路径
        backtrace(路径,选择列表)
        撤销选择,当前选择移除出选择路径
	}
}

动态规划

树

字典树

TODO

图

DFS

TODO

BFS

TODO

栈

TODO

单调栈

单调栈的核心规则就是：

➡️ 往栈里压元素时，如果破坏了单调性，就弹出栈顶直到恢复单调。

假设我们要维护“单调递减栈”（栈顶最小）：

要么 push,要么 pop 若干次，再 push,永远保持“单调递减”。

类型 栈里从栈底到栈顶 作用
单调递增栈 值越来越大 适用于找「下一个更大元素」
单调递减栈 值越来越小 适用于找「下一个更小元素」

它的核心思想是：

用单调性过滤掉无用元素，保证“最近的有效元素”在栈顶

题目

P3542 将所有元素变为 0 的最少操作次数

https://even629.com/posts/3542/

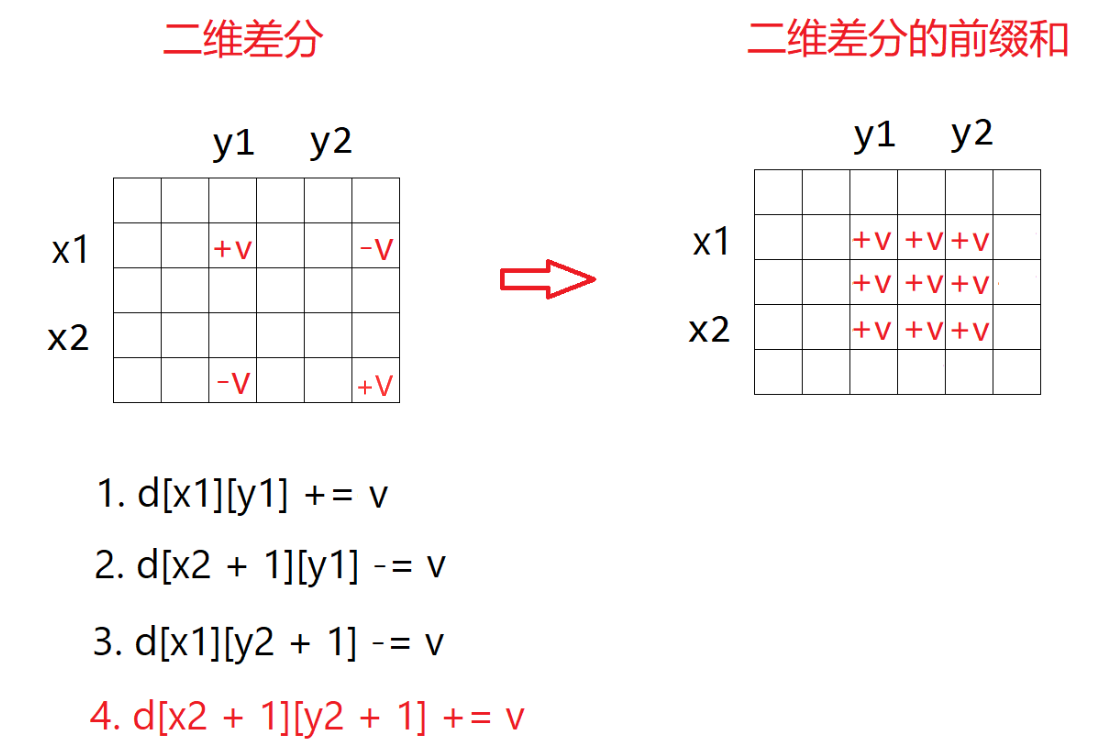
矩阵

差分与前缀和

二维差分与其前缀和

题目

P2536 子矩阵元素加一

https://even629.com/posts/2536/

排序

快速排序

Lomuto partition

每次partition确定一个值的位置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <vector>
#include <algorithm>
using std::vector;

int partition(vector<int> &arr, int start, int end)
{ // 分区区间 [l, r]
        int pivot = arr[end];
        int i = start; // 小于 pivot 的区域右边界

        for (int j = start; j < end; j++) {
                if (arr[j] < pivot) { // 小于 pivot 的放左边
                        std::swap(arr[i], arr[j]);
                        i++;
                }
        }
        std::swap(arr[i], arr[end]); // pivot 放到正确位置
        return i; // 返回 pivot 的最终位置
}

void quick_sort(vector<int> &arr, int start, int end)
{
        if (start >= end)
                return;
        int p = partition(arr, start, end);
        quick_sort(arr, start, p - 1);
        quick_sort(arr, p + 1, end);
}

#include <stdio.h>
int main()
{
        vector<int> arr = { 1, 3, 6, 2, 3, 8, 4, 9, 0 };
        quick_sort(arr, 0, arr.size() - 1);
        for(int num: arr){
                printf("%d ", num);
        }
        printf("\n");
}

Hoare partition

它并不要求 pivot 最终落在正确位置，而是保证：

  • $[start .. left-1] < pivot$
  • $[left .. end] >= pivot$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include <vector>
using std::vector;


// 4、5、8、1、7、2、6、3 // pivot = 4, left = arr[0]=4 right=arr[n-1] =3

// 3, 5, 8, 1, 7, 2, 6, 4 // left->5  right->6

// 3, 2, 8, 1, 7, 5, 6, 4 // left->8  right->7

// 3, 2, 1, 8, 7, 5, 6, 4 // left->1 right->8  right<left, stop

/*
* Hoare partition 的正常逻辑，它并不要求 pivot 最终落在正确位置，而是保证：
* [start .. left-1] < pivot
* [left .. end] >= pivot
 */

int partition(vector<int> &arr, int start, int end)
{
        int pivot = arr[start];
        int left = start, right = end;

        while (left <= right) {
                while (arr[left] < pivot) {
                        left++;
                }
                while (arr[right] > pivot) {
                        right--;
                }
                if (left <= right) {
                        std::swap(arr[left], arr[right]);
                        left++;
                        right--;
                }
        }
        return left;
}

void quick_sort(vector<int> &arr, int start, int end)
{
        if (start >= end) {
                return;
        }
        int p;
        p = partition(arr, start, end);
        quick_sort(arr, start, p - 1);
        quick_sort(arr, p, end);
}

#include <stdio.h>
int main()
{
        vector<int> arr = { 1, 3, 6, 2, 3, 8, 4, 9, 0 };
        quick_sort(arr, 0, arr.size() - 1);
        for(int num: arr){
                printf("%d ", num);
        }
        printf("\n");
}

也可以这样写

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
// 快速排序函数（Hoare 分区方案实现）
void quickSort(vector<int>& nums, int l, int r) {
    // 1. 递归终止条件：当子数组长度为1或空时，无需排序
    if (l >= r) return;

    // 2. 初始化分区参数：
    // - i 初始在左边界左侧（l-1）
    // - j 初始在右边界右侧（r+1）
    // - 基准值 x 选中间元素（避免极端情况如全排序数组导致最坏时间复杂度）
    int i = l - 1, j = r + 1;
    int x = nums[(l + r) >> 1]; // 位运算代替 (l + r) / 2，等价且更高效

    // 3. Hoare 分区循环：双指针从两端向中间移动
    while (i < j) {
        // 3.1 移动左指针 i：跳过所有小于 x 的元素，直到找到 >=x 的元素
        do i++; while (nums[i] < x);

        // 3.2 移动右指针 j：跳过所有大于 x 的元素，直到找到 <=x 的元素
        do j--; while (nums[j] > x);

        // 3.3 如果指针未交错，交换左右指针的元素（确保左边 <=x，右边 >=x）
        if (i < j) swap(nums[i], nums[j]);
    }

    // 4. 递归排序左右子数组：
    // - 分区点为 j（因为当 i >= j 时，j 是左半部分的最右端）
    // - 左子数组：[l, j]（所有元素 <=x）
    // - 右子数组：[j+1, r]（所有元素 >=x）
    quickSort(nums, l, j);
    quickSort(nums, j + 1, r);
}

堆排序

对完全二叉树结点进行编号，有如下关系

项目 1-based 编号（根=1） 0-based 编号（根=0）
左孩子 $\text{left}(i)=2i $ $ \text{left}(i)=2i+1 $
右孩子 $ \text{right}(i)=2i+1 $ $ \text{right}(i)=2i+2 $
父节点 $ \text{parent}(i)=\lfloor i/2 \rfloor（i>1）$ $ \text{parent}(i)=\lfloor (i-1)/2 \rfloor（i>0）$
至少有左孩子的条件 $ 2i \le n $ $ 2i+1 < n $
右孩子存在条件 $ 2i+1 \le n $ $ 2i+2 < n $
叶节点条件 $i > \lfloor n/2 \rfloor$ $ i > \lfloor (n-2)/2 \rfloor $或 $2i+1 \ge n$
只有左孩子条件 $2i = n $ $ 2i+1 < n $ 且 $ 2i+2 \ge n $
深度（root 层=1） $ \lfloor \log_2 i \rfloor +1 $ $ \lfloor \log_2 (i+1) \rfloor +1 $
深度（root 层=0） $ \lfloor \log_2 i \rfloor $ $ \lfloor \log_2 (i+1) \rfloor $ 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <vector>
using std::vector;

void heapify(vector<int> &vec, int curr, int n)
{
        int left = curr * 2 + 1;
        int right = curr * 2 + 2;
        int largest = curr;

        if (left < n && vec[left] > vec[largest]) {
                largest = left;
        }

        if (right < n && vec[right] > vec[largest]) {
                largest = right;
        }

        if (largest != curr) {
                std::swap(vec[largest], vec[curr]);
                //由于交换了父节点和子节点，因此可能对子节点的子树造成影响，所以对子节点的子树进行调整。
                heapify(vec, largest, n);
        }
}

void buildMaxHeap(vector<int> &vec)
{
        int n = vec.size();
        // 最后一个节点的位置为n-1，所以父节点的位置为(n-1-1)/2。
        for (int i = (n - 2) / 2; i >= 0; i--) {
                heapify(vec, i, n);
        }
}

#include <stdio.h>

int main()
{
        vector<int> nums = { 9, 8, 2, 1, 5, 3, 0, 10, 22, 5 };
        int n = nums.size();
        buildMaxHeap(nums);

        for (int i = 0; i < n; i++) {
                // pop
                std::swap(nums[0], nums[n - i - 1]);
                heapify(nums, 0, n - i - 1); // 堆长度为 n-i-1
        }
        // 输出已排序数组
        for (int i = 0; i < n; i++)
                printf("%d ", nums[i]);
        printf("\n");
}